Shift y=tan (2x5) Function Shift Calculator Symbolab Line Equations Line Given Points Given Slope & Point Slope Slope Intercept Form Distance MidpointWhat are the maximum and minimum turning points of the graph with equation \(y = 2\sin 3x 1\)?2/3/13 · for y = tan kØ , the period of the tangent curve is π/k (notice that this differs from the period definition for sine and cosine) so the period of tan (2xπ) is π/2 radians or 90° We know that tan (π/2) is undefined (a vertical asymptote) so 2x π = π/2 2x = 3π/2 x = 3π/4 So your function will have a vertical asymptote at

Graphs Of The Circular Functions Ppt Download
Graph y equals tan 2x
Graph y equals tan 2x-8/3/18 · Note Constraint −2π < x < 2π Parent graph of y = f (x) = tan(x) is also available in color RED for comparison Graph of the given function y = f (x) = tan( x 2) is in BLUE xintercepts They happen within the periods of 2π ie, ( − 4π, −2π,0,2π,4π) etcQuestion Since The Period For Y = Tan X Is 7, The Graph Of Y = Tan X Will Go Through One Complete Cycle Every A Units Through How Many Cycles Will The Graph Of Y = Tan 2x Go Every N Units?



How To Graph Tan Ex Y Tan2x Study Com
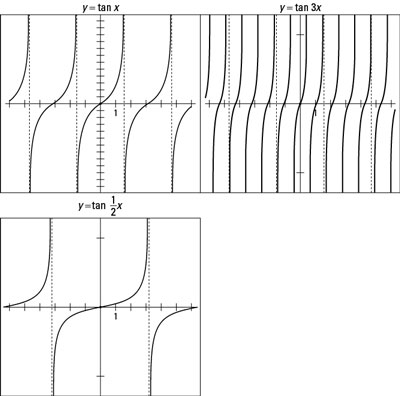
4/17/12 · The b in y=tan(bx) changes the width of the graphWhen the value of b is larger, there are more tan curves in a given period and are more steeperThe tan graph will have a longer period resulting the graph to be more wider But when the value of b is smaller, the tan curves are more narrow because of the shorter length of the periods When the values are negative, the graph isExamples Sketch the graph of one complete period 1 y= tan(2x) 2 y= tan(1 8 x) 3 y= tan(3xThe six trigonometric functions can be defined as coordinate values of points on the Euclidean plane that are related to the unit circle, which is the circle of radius one centered at the origin O of this coordinate system While rightangled triangle definitions allows for the definition of the trigonometric functions for angles between 0 and radian (90°), the unit circle definitions allow
Graph a Transformation of the Tangent Function (Period and Horizontal Shift) y = A tan (B(x D)) C • Tangent has no amplitude • π/B is the period • C is the vertical translation • D is the horizontal translation Example y = 3 tan (2x π/2) 1 Find the period of the function 2 Find the horizontal shift 3 Graph the functionY = tan − 1 (tan x) = {x − 2 π < x < 2 π } Thus, it has been defined for − 2 π < x < 2 π that has length πSo its, graph could be plotted asThe graph of y=x^22x3 represents a graph of a quadratic function On the given graph you can find all of the important points for function y=x^22x3 (if they exist)
6/21/07 · y = 2tan(x) This is just a little vertical stretching Start with the graph previously described Erase whatever you labled (pi/4,1) and relable it (pi/4,2) You're almost done Relable a few more things and move on y = 2tan(2x) This is just a little horizontal compression Start with the graph previously describedThe period of tan 2x is 2 πAnswer to Find the period y = tan(2x pi/2) Graph the function By signing up, you'll get thousands of stepbystep solutions to your homework



Graphing Transformations Of Tangent Functions Flashcards Quizlet


How Do You Identify The Period And Asympotes For Y 2tan Pitheta Socratic
Y = tan x Period This is the graph of y = tan x A cycle of a tangent is the graph between the asymptotes For the middle cycle, the asymptotes are x = ±π/2 A period is the width of a cycle So the period of y = tan x is π/2 (π/2) = πThe combined graph of sine and cosine function can be represented as follows Tan Graph The tan function is completely different from sin and cos function The function here goes between negative and positive infinity, crossing through 0 over a period of π radian y = tan x;7 and 6 4 and 3 3 and 1 9 What is the amplitude of a graph with the equation \(y = \tan 2x\)


Solution Graph Y 1 2 Tan 2x Pi 2 And The Period And Phase Shift


Graph Tangent Functions With Variable Multipliers Dummies
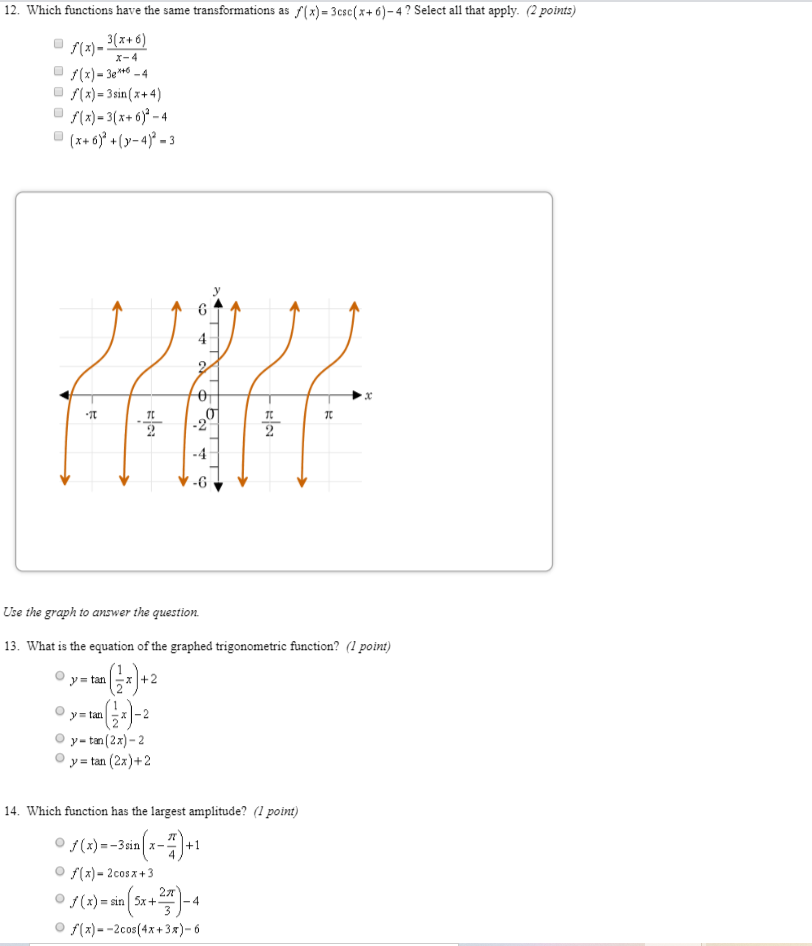
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreThe vertical asymptotes for y = tan ( x 2) y = tan ( x 2) occur at − π π, π π, and every 2 π n 2 π n, where n n is an integer x = π 2 π n x = π 2 π n Tangent only has vertical asymptotes No Horizontal Asymptotes No Oblique Asymptotes Vertical Asymptotes x = π 2 π n x = π 2 π n where n n is an integerAnswers Click here to see ALL problems on Trigonometrybasics Question y = 2 tan 2x graph two periods of the given tangent function Answer by Fombitz () ( Show Source ) You can put this solution on YOUR website!


How Do You Graph Y Tan3x Socratic


How Do You Graph Y Tan3x Socratic
Related » Graph » Number Line » \frac{d}{dx}\left(tan\left(2x\right)\right) en Related Symbolab blog posts Advanced Math Solutions – Derivative Calculator, Implicit Differentiation We've covered methods and rules to differentiate functions of the form y=f(x), where y is explicitly defined as10/27/10 · y = tan x Note The slope of the tangent curve is positive for all values of x (except the asymptotes, of course, where the curve and the slope is undefined) Graph of cos x Next we have y = cos x It has the same shape as the sine curve, but has been displaced (shifted) to the left by π/2 (or 90°) y = cos x Graph of sec x and sec 2 xThe graph of y=sin(x) is like a wave that forever oscillates between 1 and 1, in a shape that repeats itself every 2π units Specifically, this means that the domain of sin(x) is all real numbers, and the range is 1,1 See how we find the graph of y=sin(x) using the unitcircle definition of sin(x)
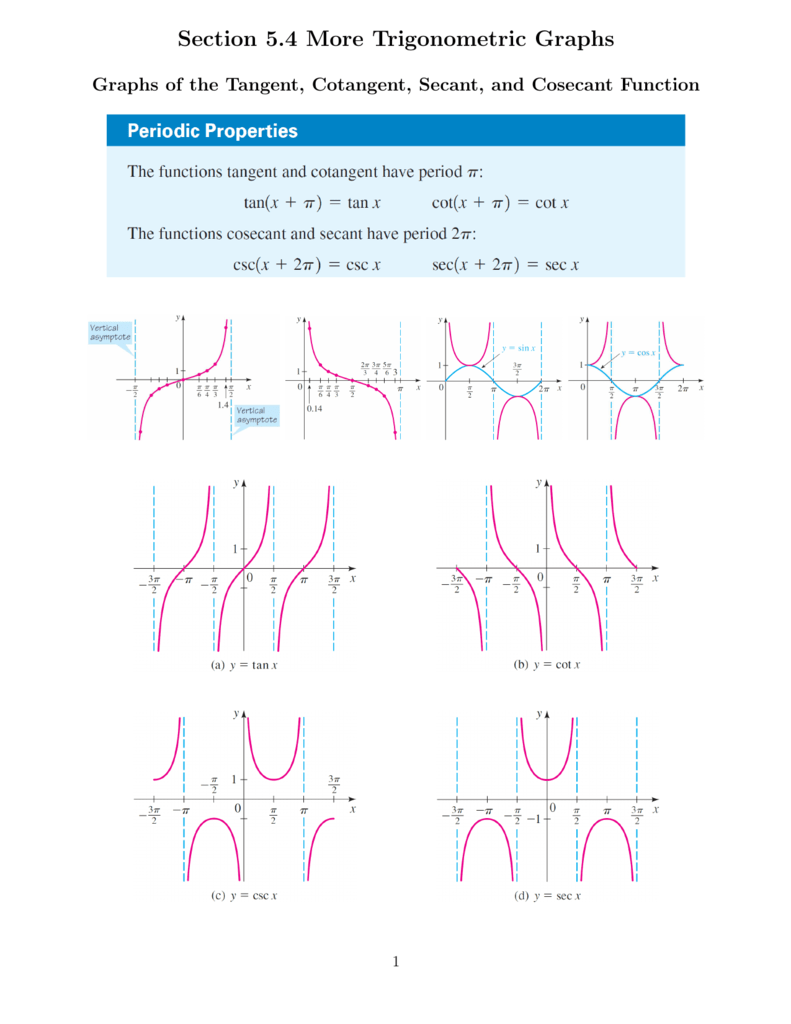


Section 5 4 More Trigonometric Graphs A To Graph Y 2 Tan X We


Solution Y 2 Tan 2x Graph Two Periods Of The Given Tangent Function
Graph the function over a oneperiod intervaly = 2 Find the vertex and yintercept and graph the equationy = 2x Graph the functiony = tan 2x asked May 6, 19 in Mathematics by Parreira algebraandtrigonometry;As b gets larger, the period of the graph getsPlease Subscribe here, thank you!!!
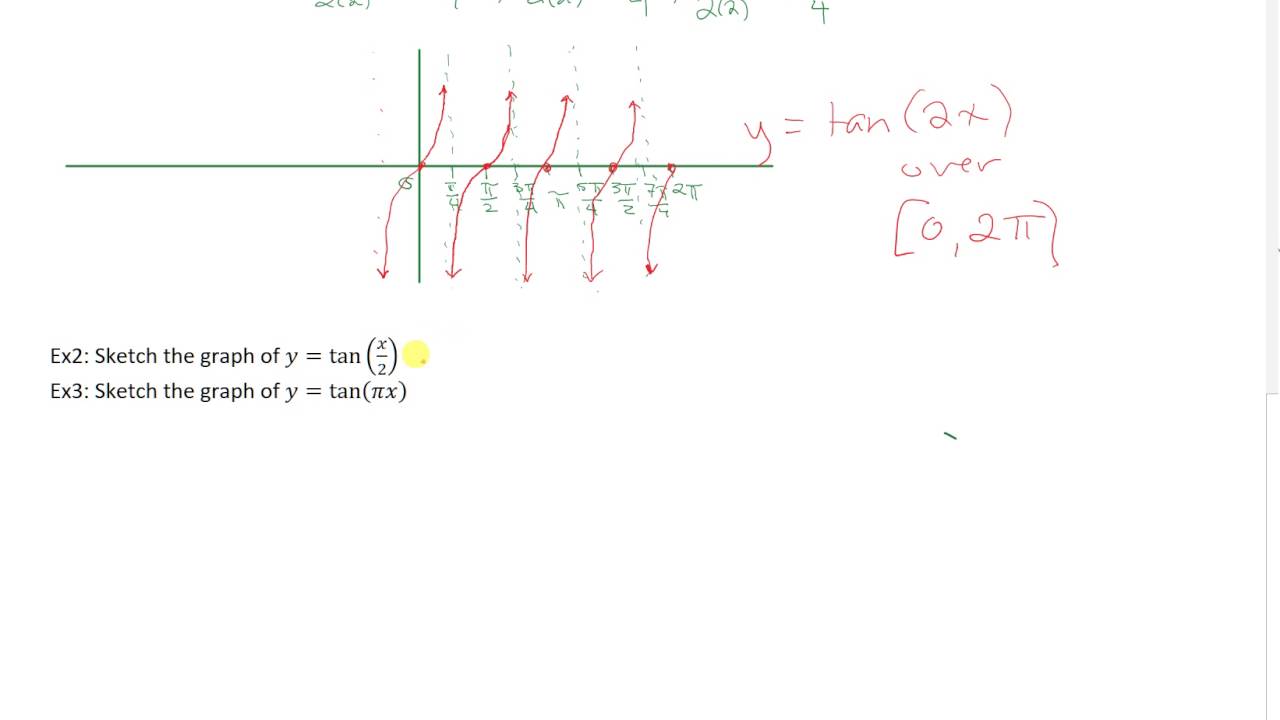


Sketching Y Tan 2x And Y Tan X 2 Youtube



Tangent Graph
Solution for Skétch the graph y = tan(2x) Find the period, asymptotes, and interceptsThe slope of the tangent line is Suppose an object is fired vertically upward from the ground on Mars with an initial velocity of 54 ft/s The height s (in feet) of the object above the ground after t seconds is given by s=54t8/12/08 · C Repeat for y = tan x, y = tan 2x and y = tan ½ x What is the period of each?
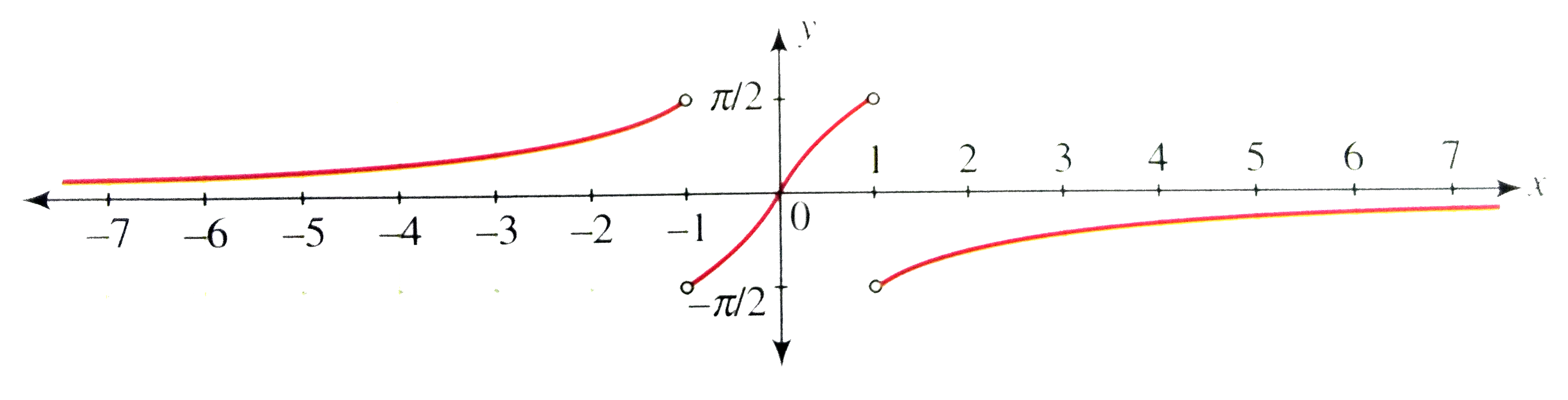


Draw The Graph Of Y Tan 1 2x 1 X 2



Graphs Of The Circular Functions Ppt Download
As y = tan − 1 (tan x) is periodic with period π ∴ to draw this graph we should draw the graph for one interval π and repeat for entire values of x As we know;What Is The Period Of Y = Tan 2x?Y = tan (2 x − 2 3 π ) Explanation Period of tan x > pi;


Trigonometry Functions User S Blog



Aim What Are The Graphs Of Tangent Function And Reciprocal Functions Ppt Video Online Download
6/28/14 · tan = O/A = 1/1 = 1 I personally don't know why they don't like irrational numbers in the denominator of fractions, but they don't So they usually convert that fraction (in both sin and cos) by multiplying by √2/√2 sin = O/H = 1/√2 = 1/√2 * √2/√2 = (1*√2) / (√2*√2) = √2/2 cos = √2/2Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyDescribe how to sketch the graph ofy = tan(2x) 3 using the parent function Start by graphing the tangent function Compress the graph horizontally by making the period onehalf pi Reflect the graph over the xaxis
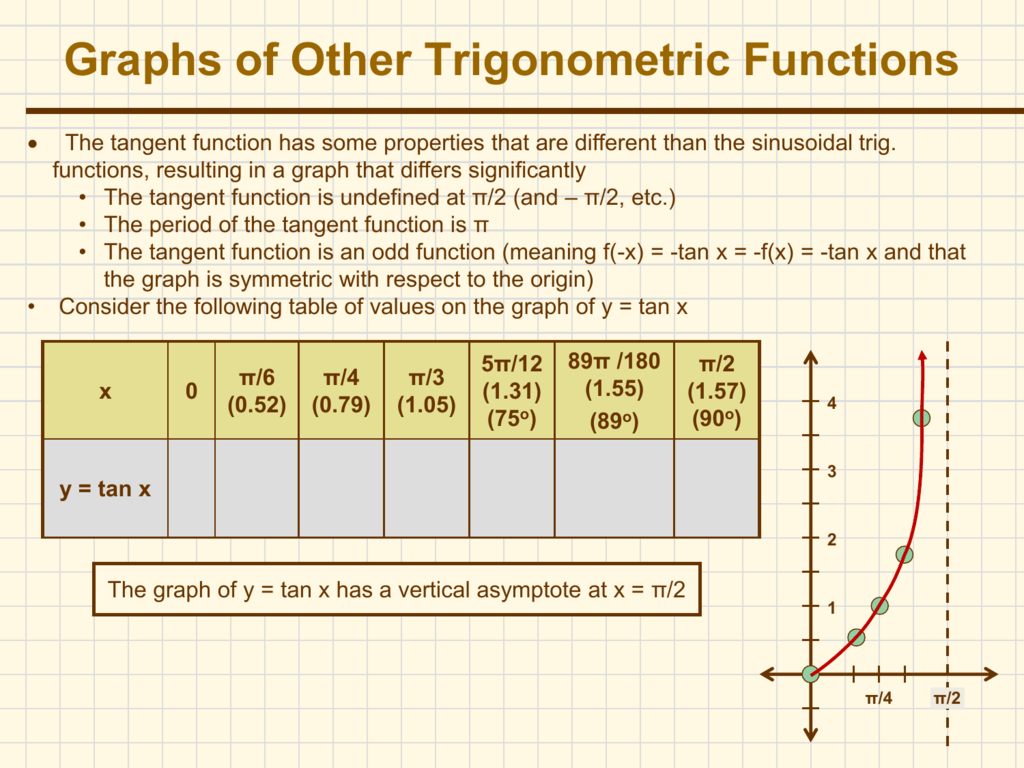


Section 4 6


Chapter 7 Trigonometric Functions The Sine Function Imagine
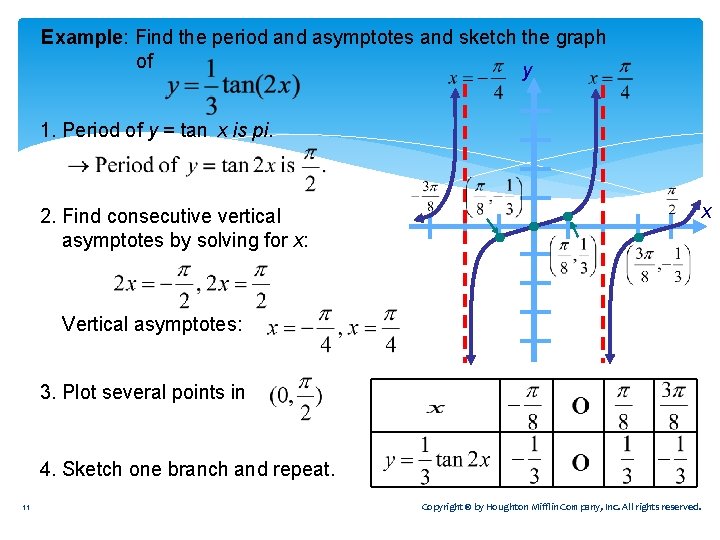
Graph and state whether each function is odd, even or neither 4 y = tan x 2 5 y = cot(x) 2 If F is any function with period 5, determine the period of each related function Provide a reason for your answer 6 y = F(x 1) 7 y = F(x) 5 8 1 y F x 2 9 y = F(3x) Graph one cycle of each function 10 4 y tan 2x 1 3 11 4 y 3csc 2x 1 3Sketch The Graph Of Y Tan 2x, From X To X = *Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history


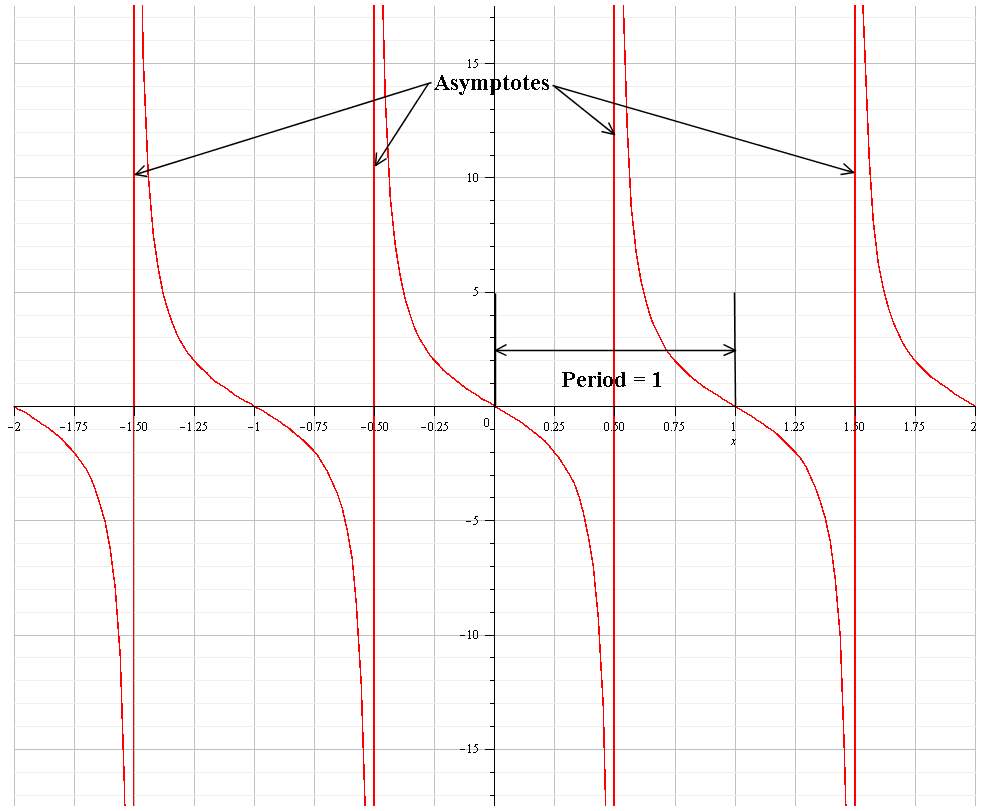
Solution Determine The Period Of Y Tan 2x


Graph Tangent And Cotangent
A xintercepts means the points on the axis where given graph cut/intersection the xaxisAnswer to How to graph tan ex y=tan2x By signing up, you'll get thousands of stepbystep solutions to your homework questions You can also askThis leaderboard is currently private Click Share to make it public This leaderboard has been disabled by the resource owner This leaderboard is disabled as



Example 4 Graph A Tangent Function Graph One Period Of The Function Y 2 Tan 3x Solution B P 3 P The Period Is Intercepts 0 0 Asymptotes X Ppt Download


Find The Period Of Tan 2x Class 10 Maths Cbse
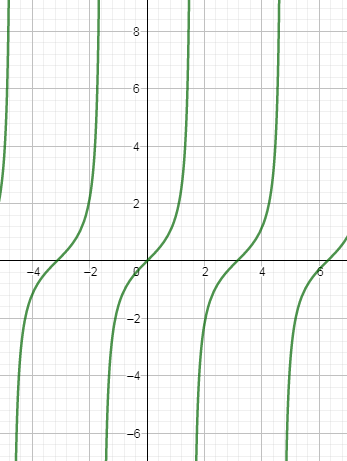
//googl/JQ8NysSketch the Graph of f(x) = tan(2xThe graph of y=tan(x^2) represents a graph of a trigonometricfunction On the given graph you can also find all of the important points for function y=tan(x^2) (if they exist)X = π 4 x = π 4 The basic period for y = tan ( 2 x) y = tan ( 2 x) will occur at ( − π 4, π 4) ( π 4, π 4), where − π 4 π 4 and π 4 π 4 are vertical asymptotes ( − π 4, π 4) ( π 4, π 4) The absolute value is the distance between a number and zero The distance between 0 0 and 2 2 is 2 2 π 2 π 2
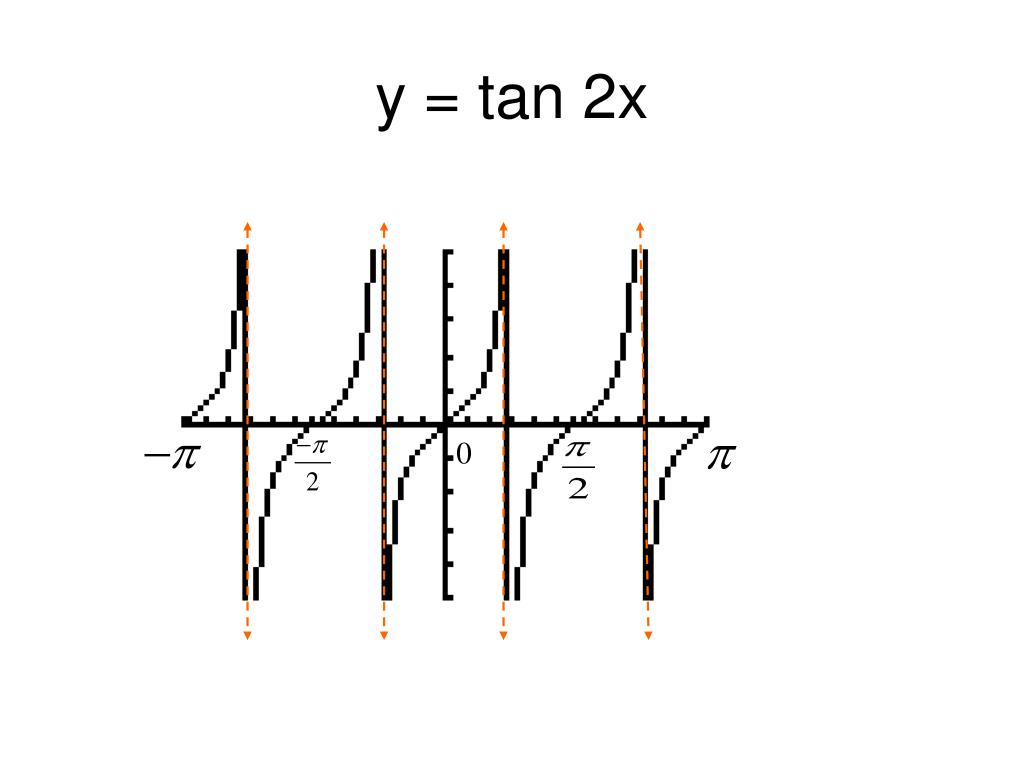


Ppt Graphing Tangent Powerpoint Presentation Free Download Id


How Do You Graph Ytan 2x Class 11 Maths Cbse
1 graph y = tanx and y = tan(x p/2) on the same coordinate plane (but in different colors) 2 Then graph y = cotx and y = cot(x p/4) on the same coordinate plane (but in different colors) Examine more graphs of this form if you find it necessary to be able to answer the following questionsThat said, however, in your particular case, plotting both $\tan x$ and $2x$ will quickly show you there are more solutions One is the zero function, the other two can be only calculated numericallyThe tangent graph has an undefined amplitude as the curve tends to
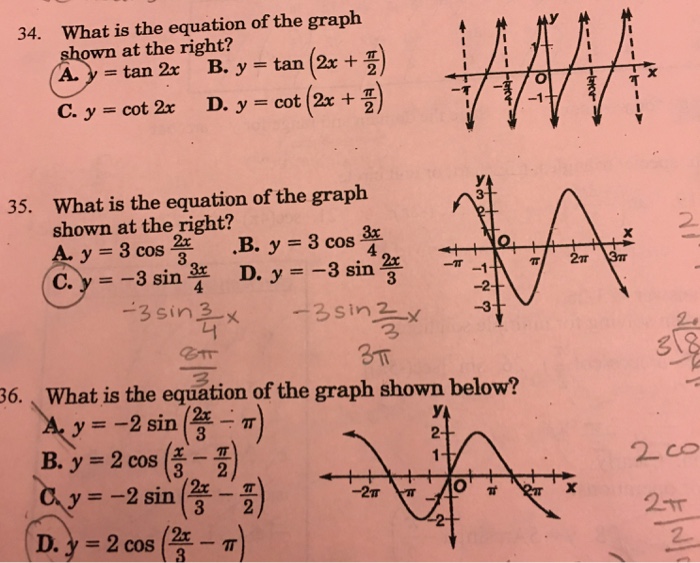


Solved What Is The Equation Of The Graph Shown At The Rig Chegg Com



How To Graph Tan Ex Y Tan2x Study Com
6/7/15 · (d) Hence or otherwise, find the coordinates of the local maximum and local minimum points of the graph of ##y = tan(2x) cot(2x), 0≤x≤\frac{π}{2}## Homework Equations Most likely a lot of different trigonometric formulas to help with this, but I'm not sure which specificallyThe graph of \(y=\tan x\) does not have an amplitude, but we can see any vertical stretch by comparing the function values at the guidepoints Example 712 Graph \(y=13\tan 2x\text{}\)Sketch the graph of y = tan(2x π/2) over one period Solution Graphing Parameters range (∞ , ∞) Period = π/k = π/2 Vertical asymptotes are found by solving for x the equation 2x π/2 = π/2 kπ which gives x = kπ/2 , k = 0 , ~mn~1, ~mn~2,


6 2 Graphs Of Sine Cosine And Tangent Spm Mathematics
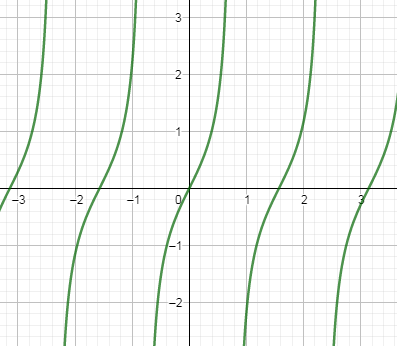


How Do You Graph Ytan 2x Class 11 Maths Cbse
What is the slope of the line tangent to the graph of y=tan (2x) at x = 1?4/15/18 · The graph of `y=tan(x)` for `pi/2 ≤ x ≤ 2pi` Note that there are vertical asymptotes (the gray dotted lines) where the denominator of `tan x` has value zero (An asymptote is a straight line that the curve gets closer and closer to, without actually touching it//googl/JQ8NysSketch the Graph of f(x) = tan(2x) Please Subscribe here, thank you!!!



Draw The Graph Of Y Tan2x Y Tan3x And Y 2cot2x Maths Trigonometric Functions Meritnation Com


Biomath Trigonometric Functions
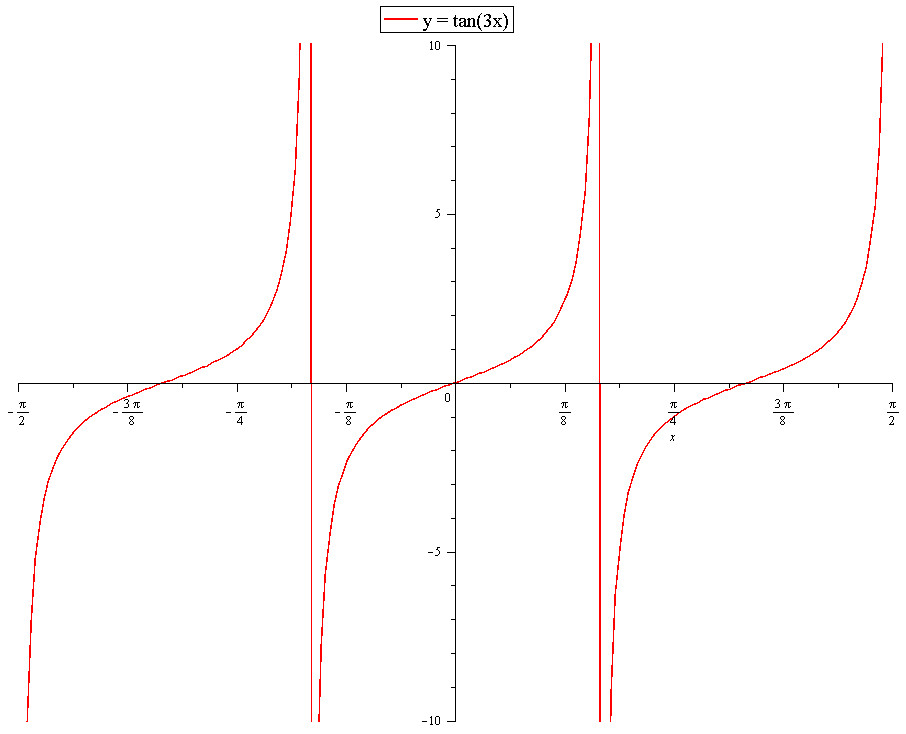
Welcome to Sciemce, where you can ask questions and receive answers from other members of the communityGraph y=3tan (2x) Equation of tan function y=Atan (BxC), period=π/B, phase shift=C/B, A is a multiplier that stretches the curve vertically For given equation y=3tan (2x) A=3 B=2 period=π/B=π/2 1/4 period=π/8
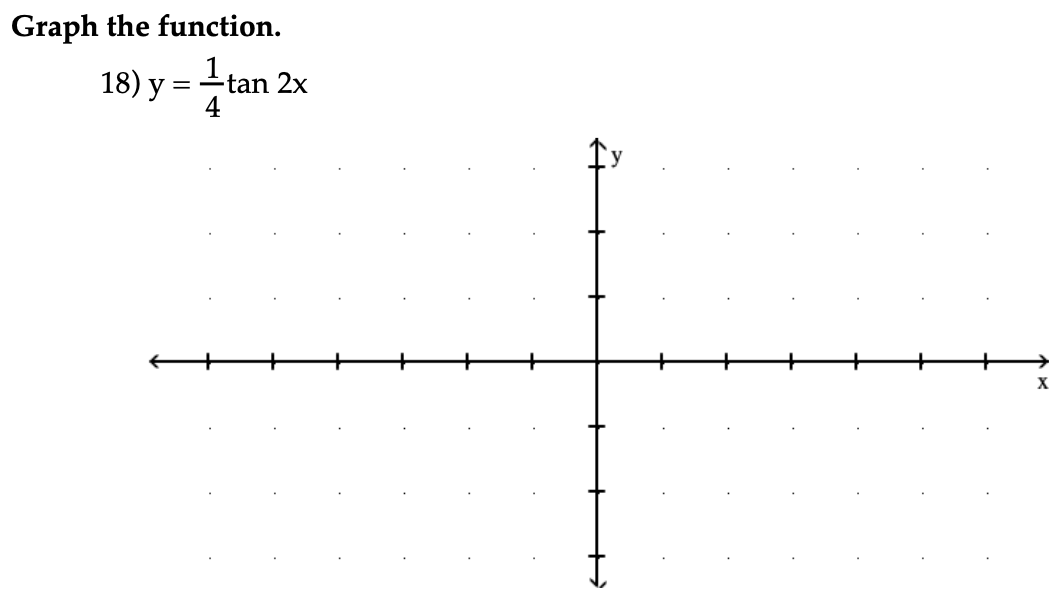


Answered Graph The Function 18 Y Tan 2x Bartleby



The Tangent Function Functions Siyavula



Graphing Tangent Read Trigonometry Ck 12 Foundation
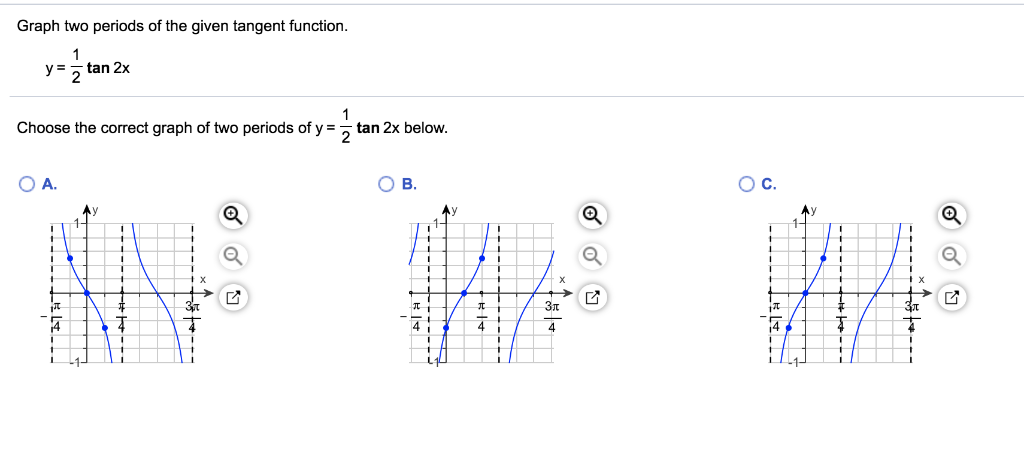


Solved Graph Two Periods Of The Given Tangent Function Y Chegg Com


Solved The First Possibility Should Be Y Tan X Not Y Tan Chegg Com
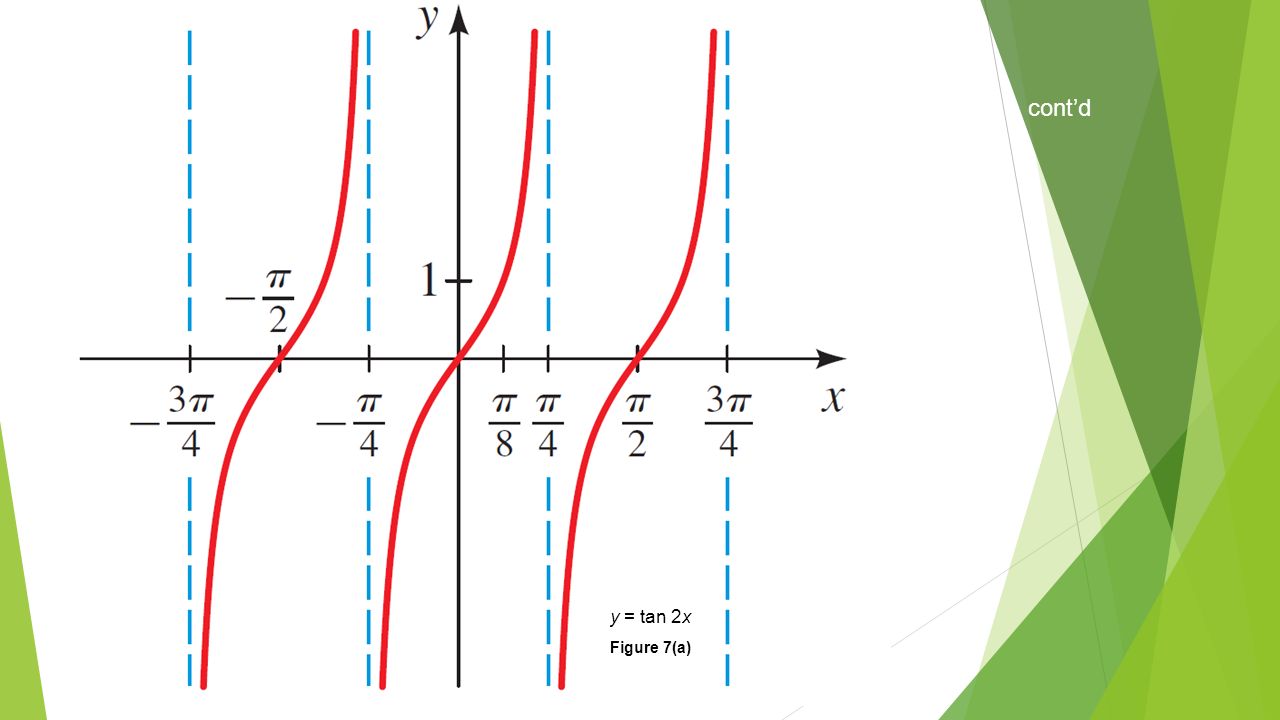


Graphs Of Tangent Cotangent Ppt Video Online Download



Aim What Are The Graphs Of Tangent Function And Reciprocal Functions Ppt Download



Solved Sketch The Graph Of The Following Functions Y Tan 2x Y Self Study 365


Howto How To Find Vertical Asymptotes Of Tan2x Cute766


What Is The Period Of This Function Sin4x Tan2x Quora


Solution Show Me The Graph Of Y Tan2x Step By Step And How To Solve Keypoints



Tangent Graphs Worked Solutions Examples Videos
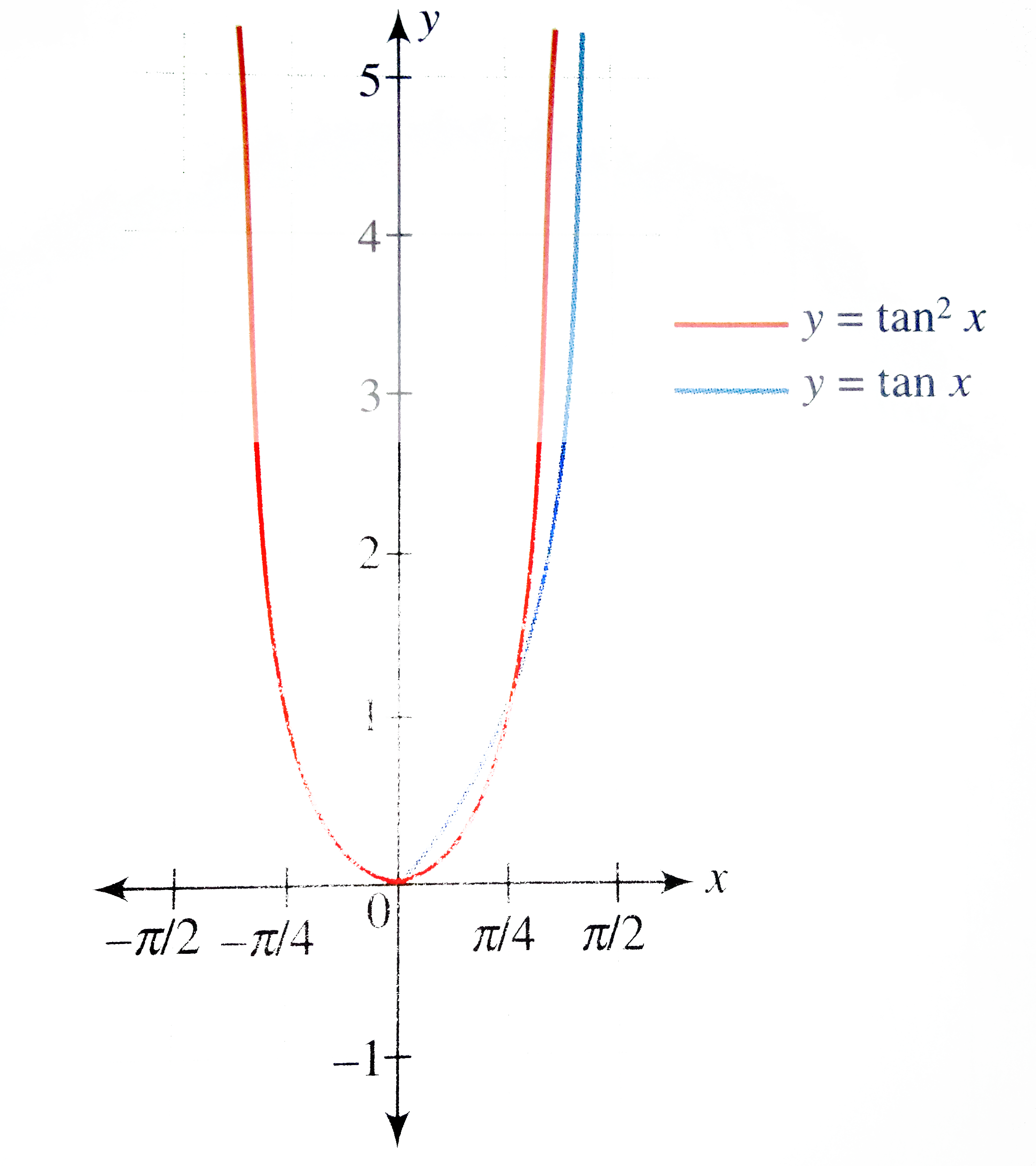


Draw The Graph Of Y Tan 2 X
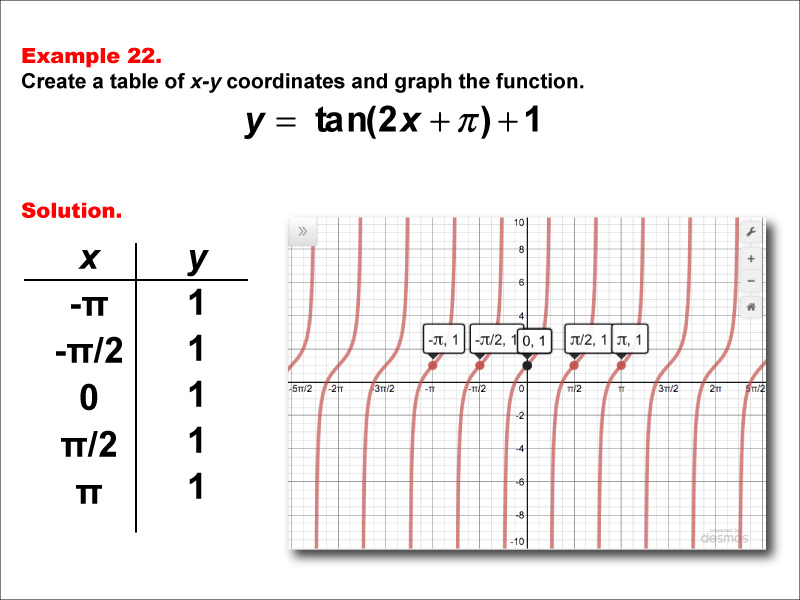


Math Example Tangent Functions In Tabular And Graph Form Example 22 Media4math



The Tangent Function Functions Siyavula
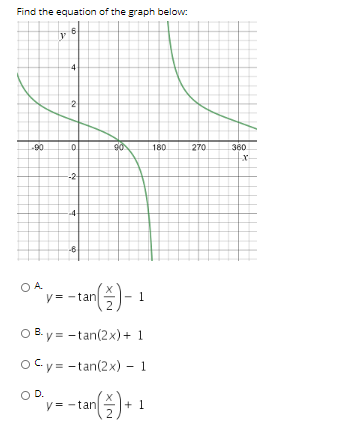


Solved Find The Equation Of The Graph Below V On 4 2 90 Chegg Com
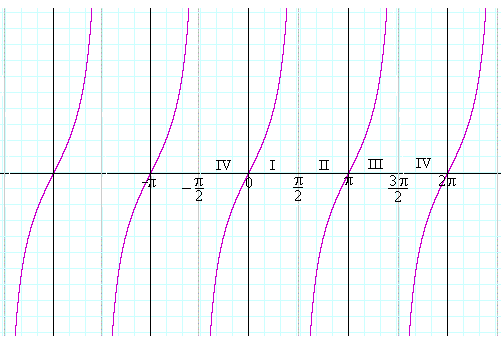


Graphs Of Trigonometric Functions



Sketch The Graph Of The Tangent Curve Y Tan 2x In The Interval From 0 To 2pi Brainly Com
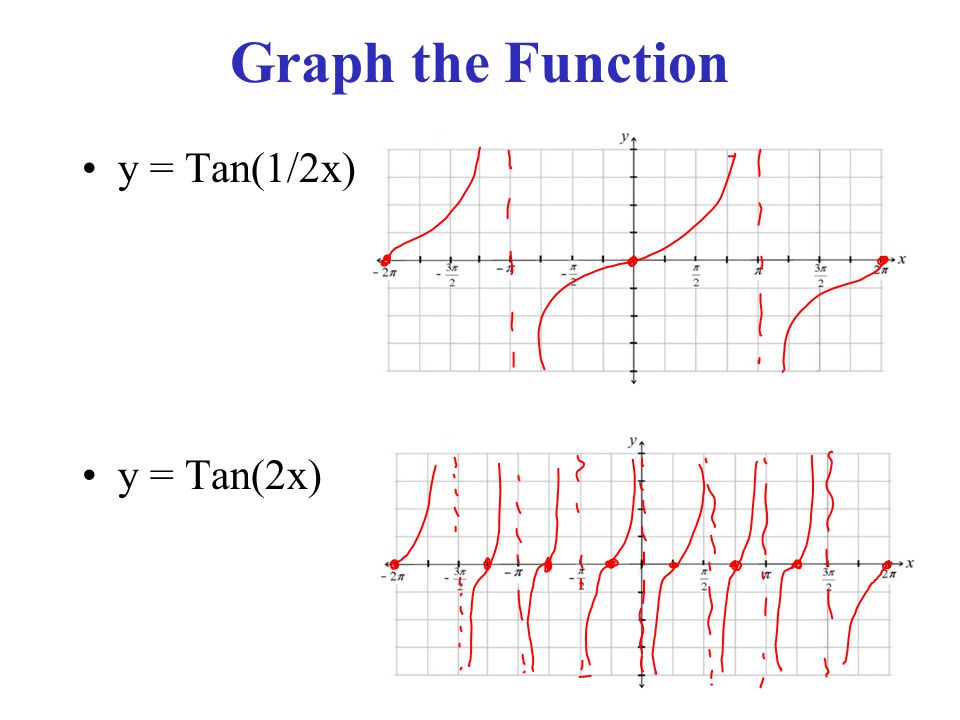


Warm Upnov 25 Th Determine Whether To Us The Law Of Sine Or Cosine And Solve For The Missing Pieces 1 D Abc With A 12 B 13 C 24 2 D Abc Ppt Download


What Is The Period Of The Function Tan 2x 6
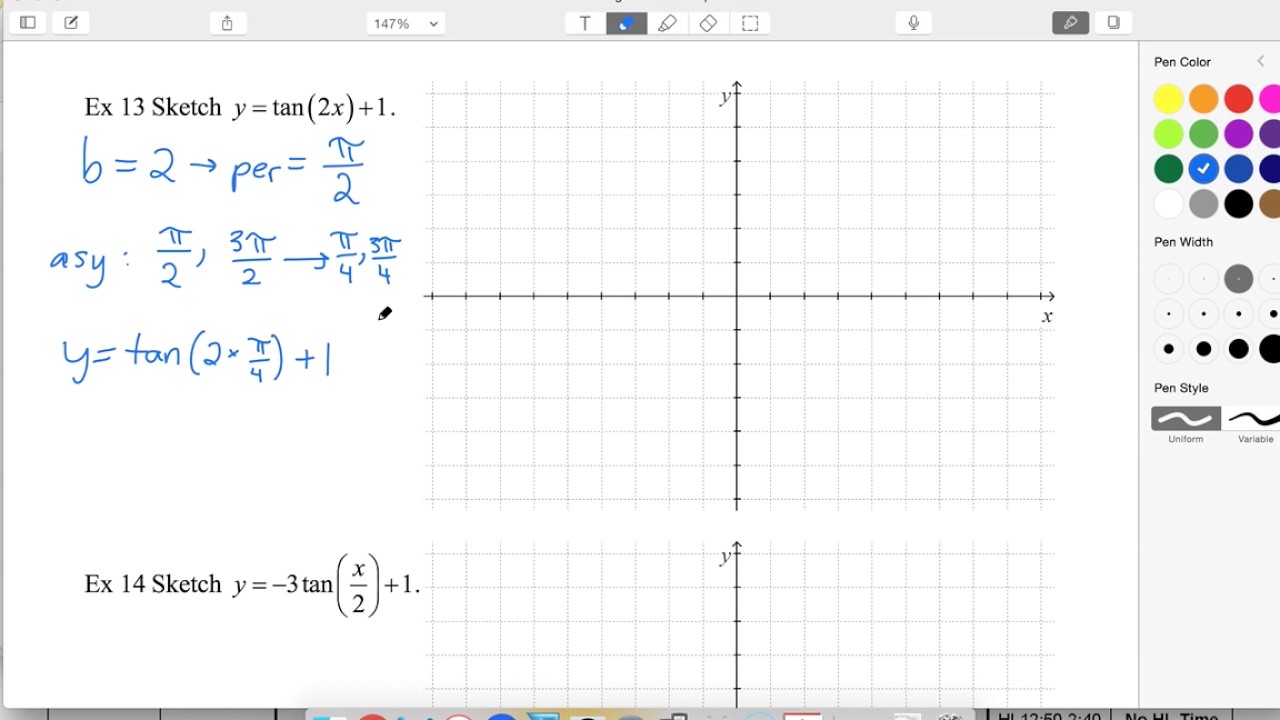


01 Ex13 Sketch Y Tan 2x 1 Youtube


Graphs Of The Other Trigonometric Functions Precalculus Ii
.png)


Sketch The Graph Of The Following Function On The Same Scale 10 Y Tan 2x Y Maths Meritnation Com
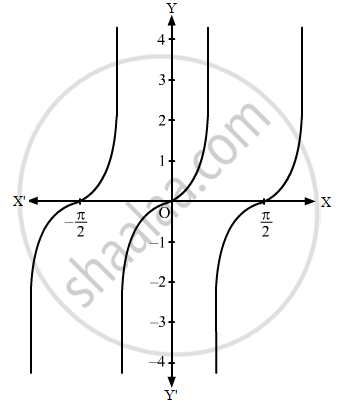


Sketch The Graphs Of The Following Functions F X Tan 2x Mathematics Shaalaa Com
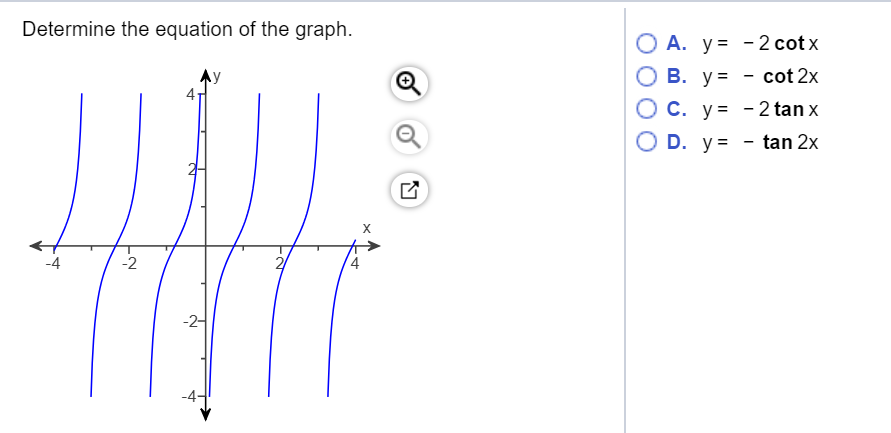


Solved Determine The Equation Of The Graph 2 Cotx Ov U Chegg Com
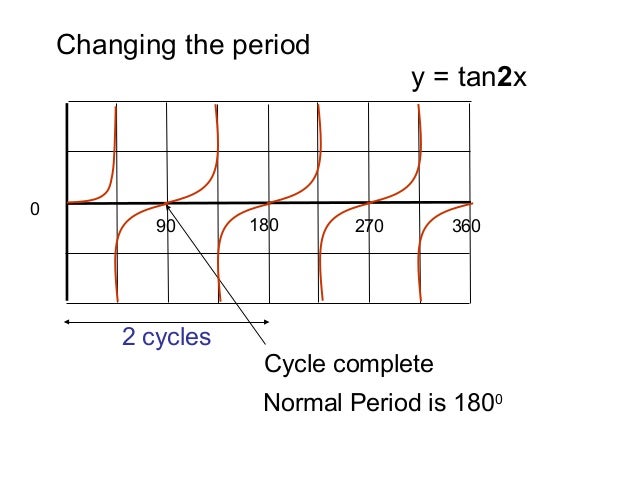


Trigonometric Graphs


Draw Tangent Graph Y Tan X Mathematics


Graph Tangent And Cotangent
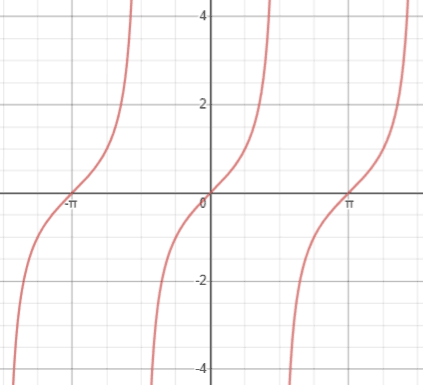


Tangent
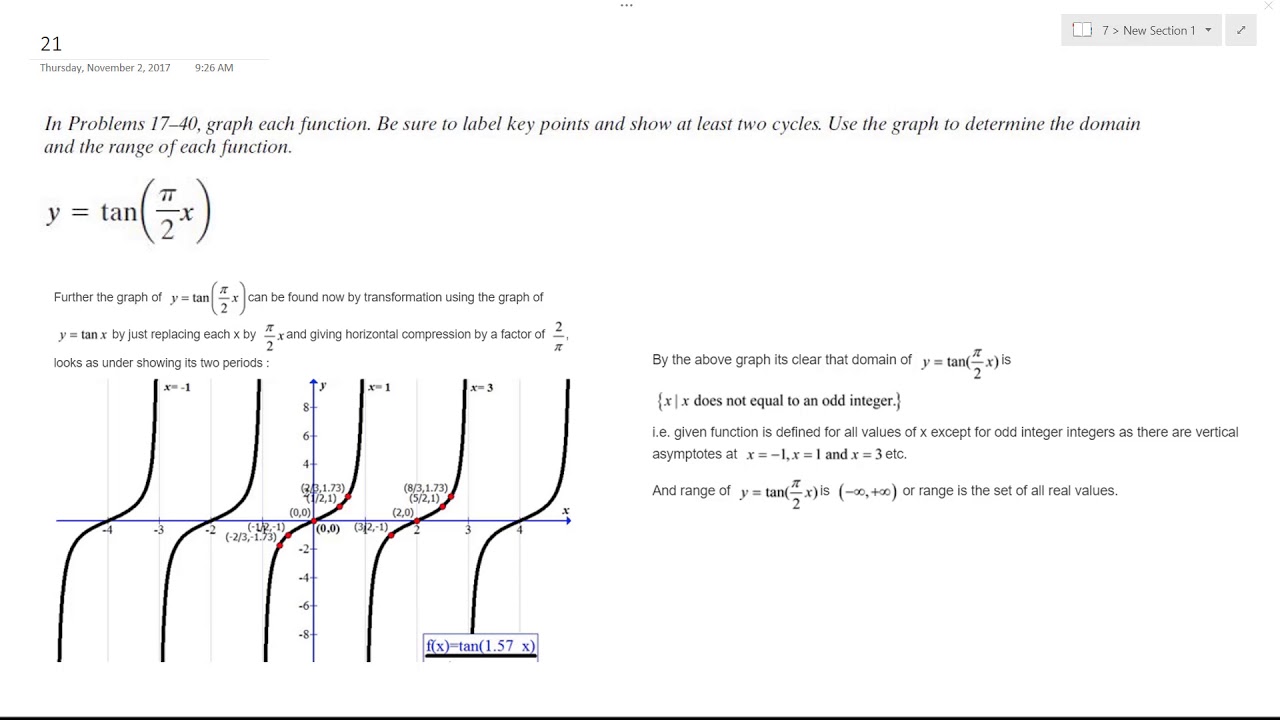


Y Tan Pi 2 X Graph And Label For 2 Cycles Youtube



Describe The Transformations Of The Following Function Y Tan 2x P Brainly Com
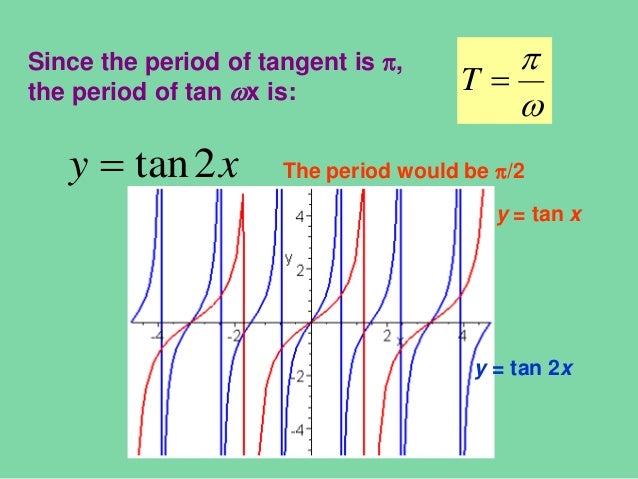


Graphs Of Other Trigonometric Functions Lecture
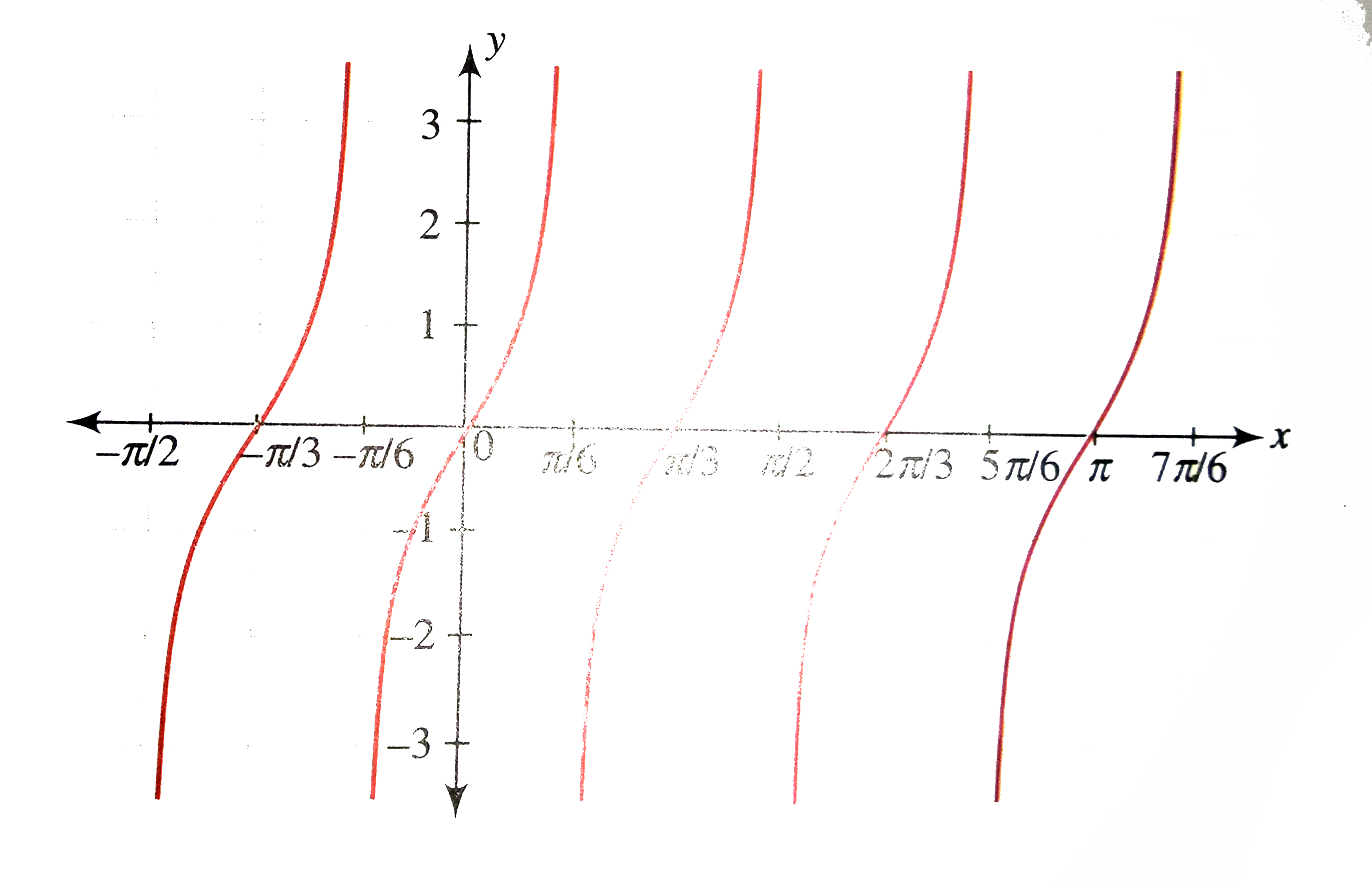


Draw The Graph Of Y Tan 3x
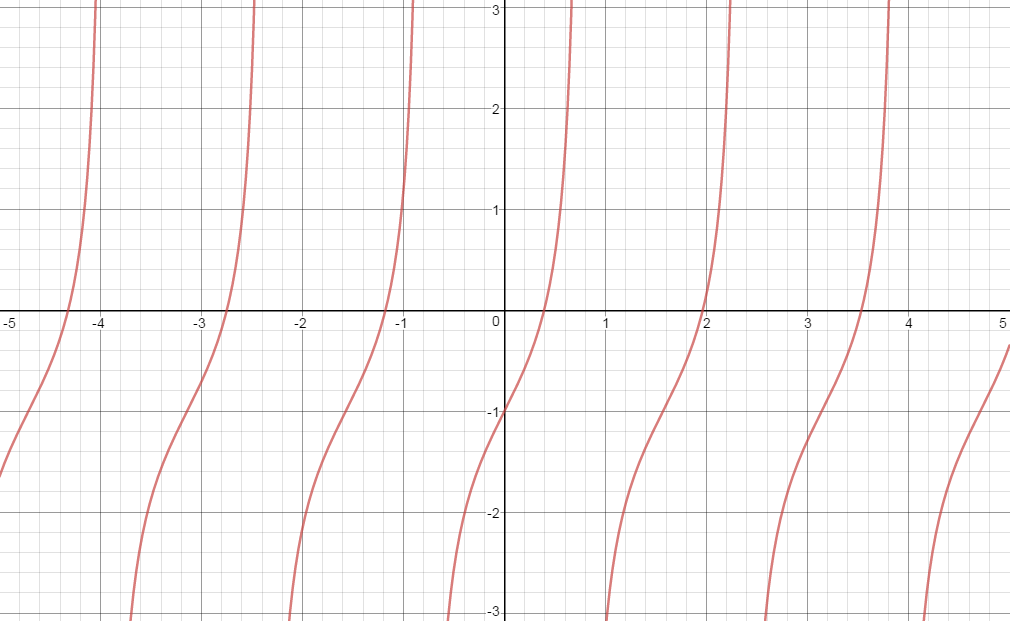


How Do You Graph Y 1 Tan2x Socratic


Graph Tangent And Cotangent
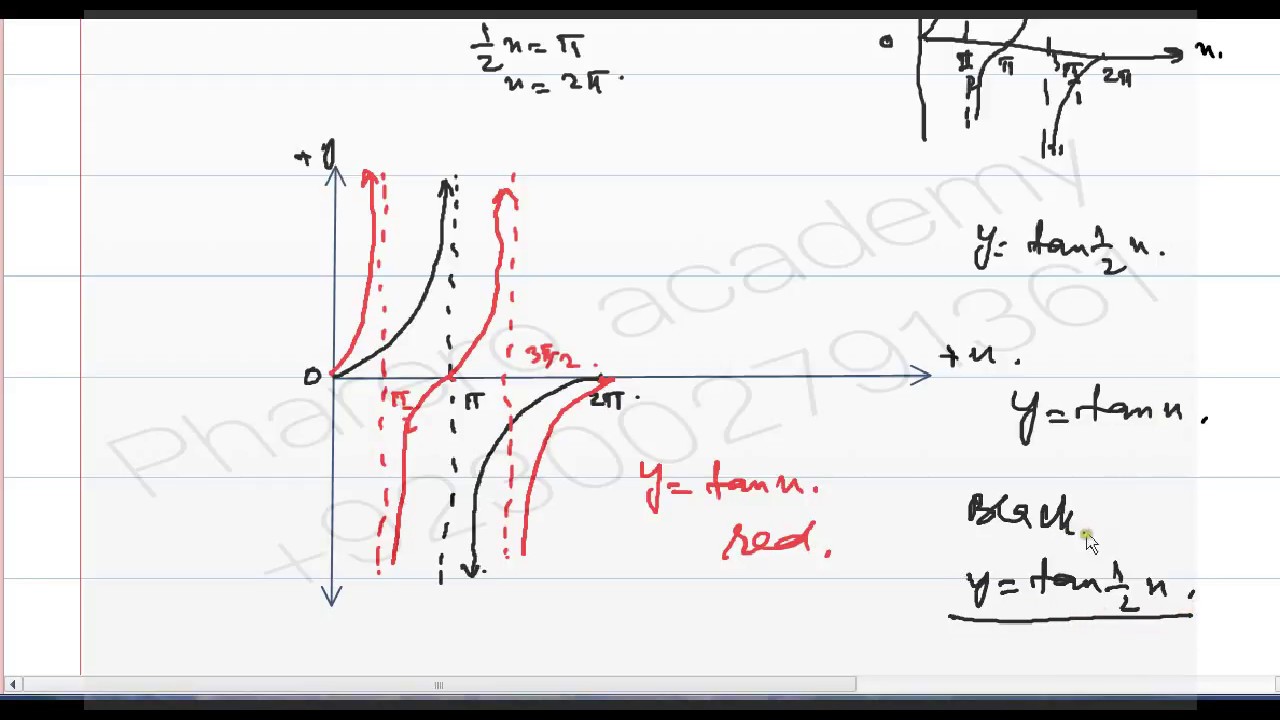


Graph Of Y Tan 1 2 X In Urdu Hindi Youtube



What Function Represented By Graph Answer Choices Y Tan 2 Theta Y Tan 1 2 Theta Y Tan Theta Y Tan Brainly Com



How To Graph Tan Ex Y Tan2x Study Com



Graphing The Tangent Function Amplitude Period Phase Shift Vertical Shift Video Lesson Transcript Study Com
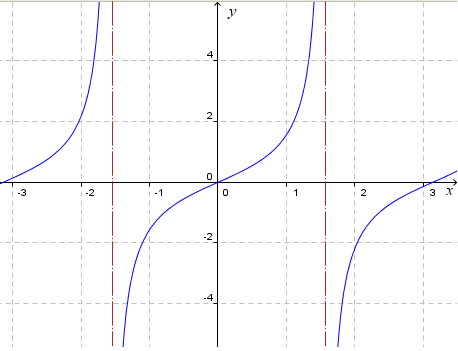


Explore The Slope Of The Tan Curve
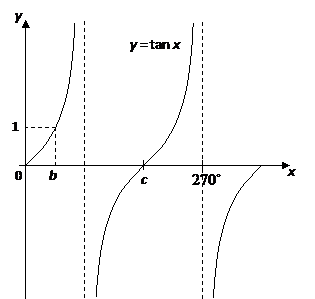


Tangent Graphs Worked Solutions Examples Videos



Graphing Tangent Read Trigonometry Ck 12 Foundation


Sketch The Graph Of F X Tan 2x Youtube



Solved Graph The Function Over One Period Interval Y Ta Chegg Com
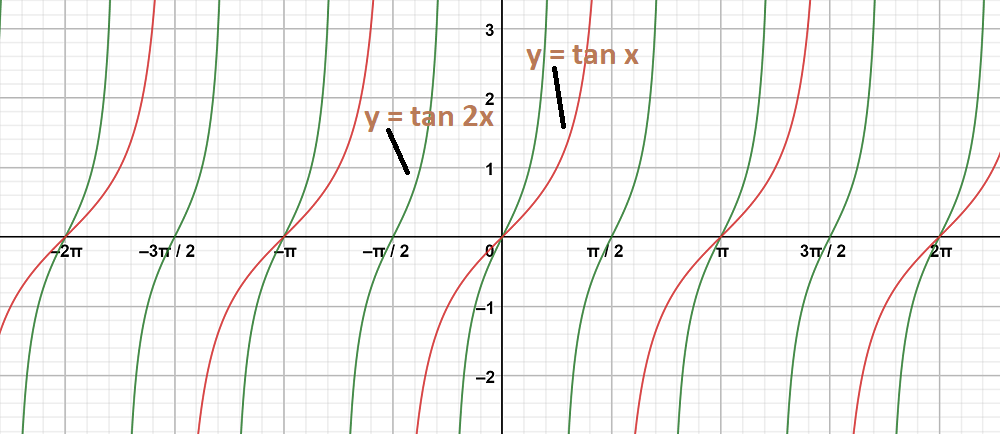


Class 11 Rd Sharma Solutions Chapter 6 Graphs Of Trigonometric Functions Exercise 6 3 Geeksforgeeks
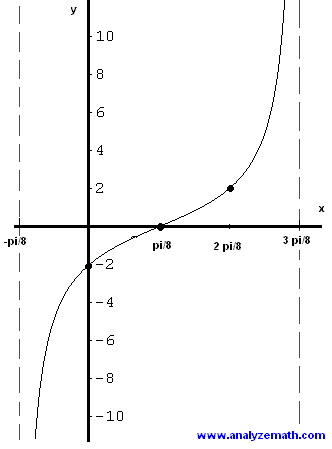


Graphing Tangent Functions
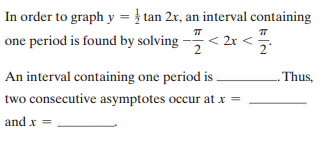


Answered In Order To Graph Y Tan 2x An Bartleby
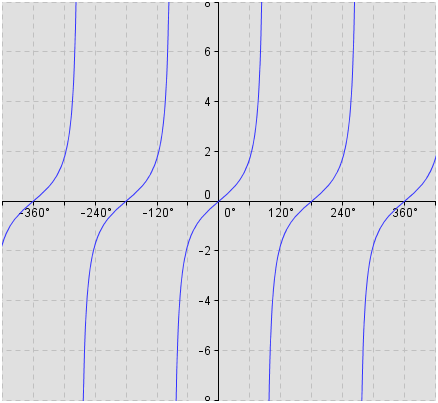


Trigonometry Trigonometric Functions
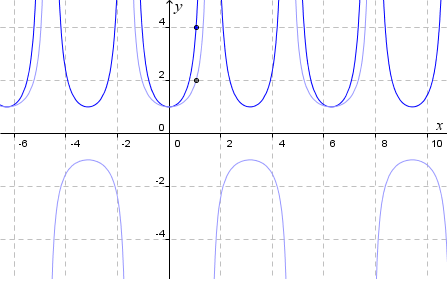


Explore The Slope Of The Tan Curve


Tangent Graphs
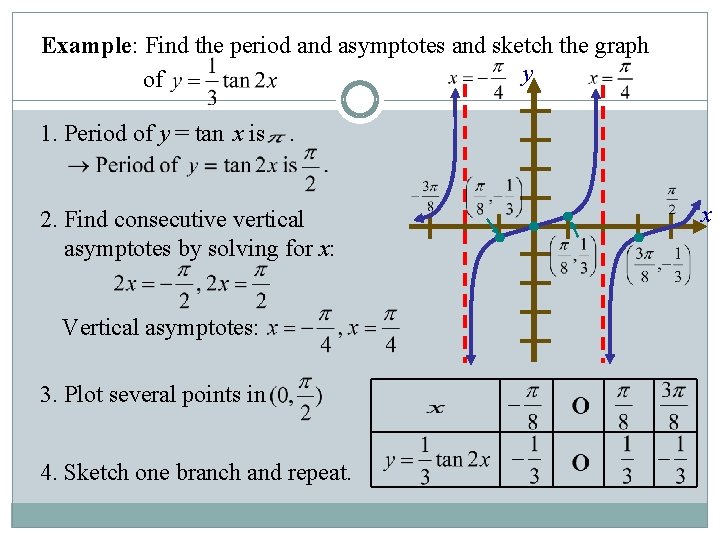


Unit 7 Trigonometric Functions Graphing The Trigonometric Function



Solved What Is The Slope Of The Tangent Line To The Graph Chegg Com
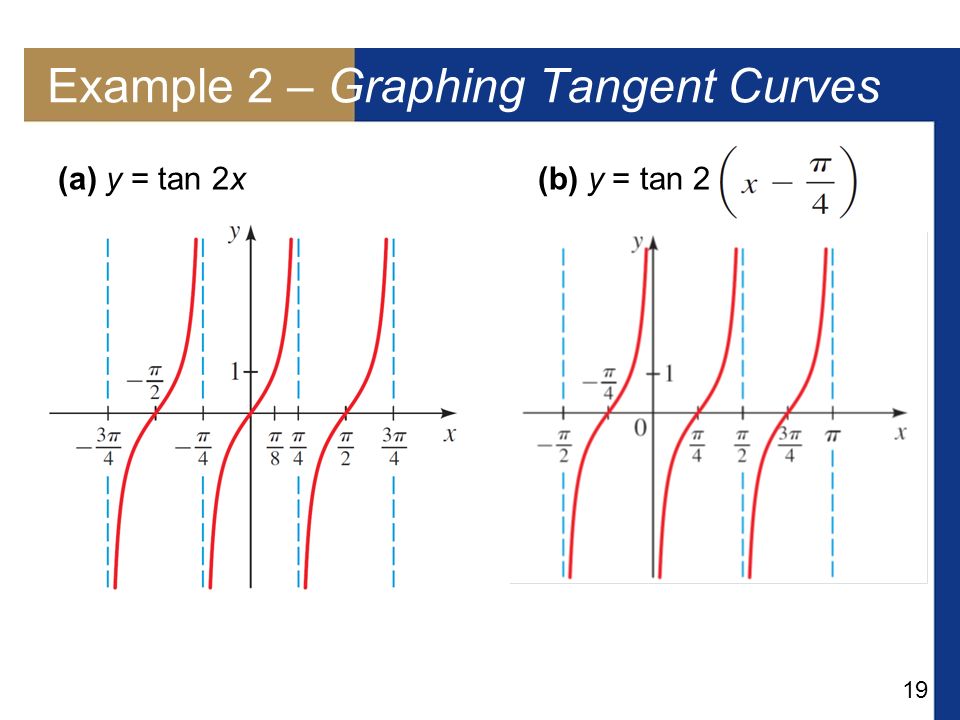


More Trigonometric Graphs Ppt Download
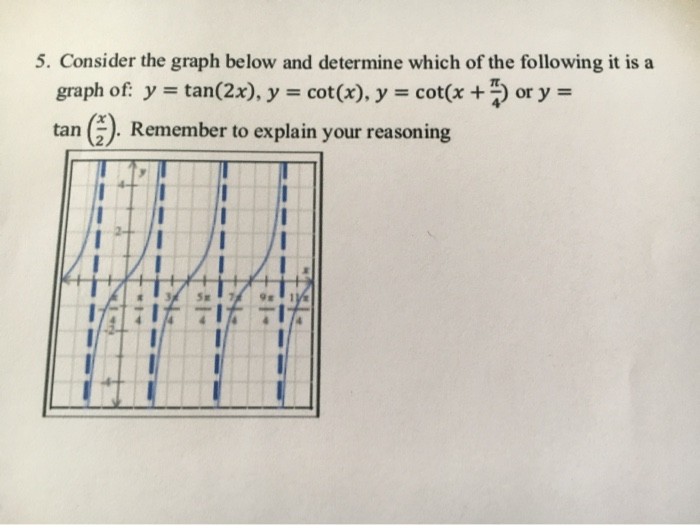


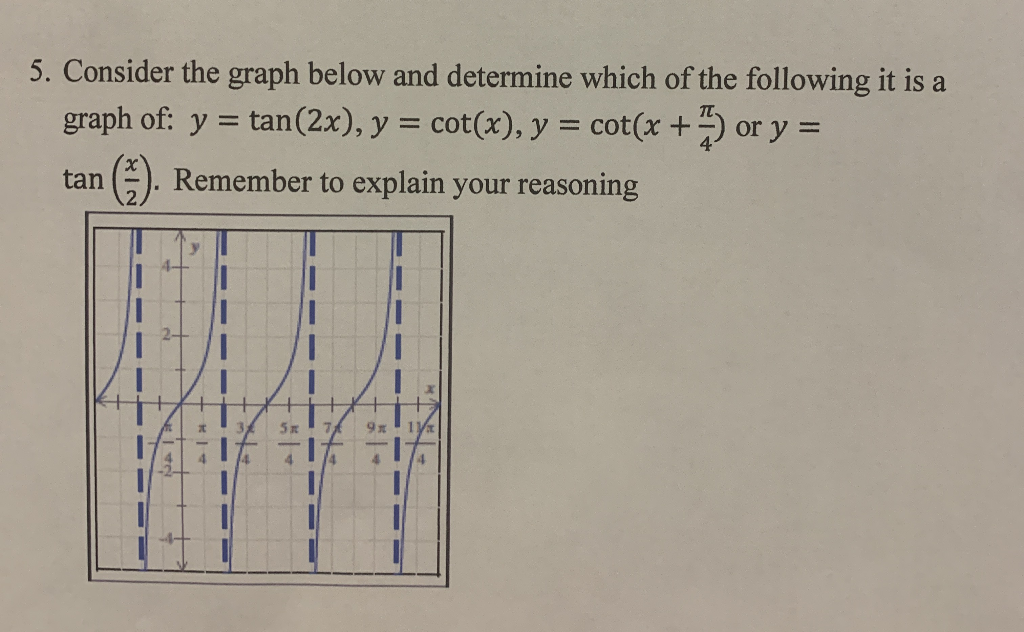
Solved 5 Consider The Graph Below And Determine Which Of Chegg Com
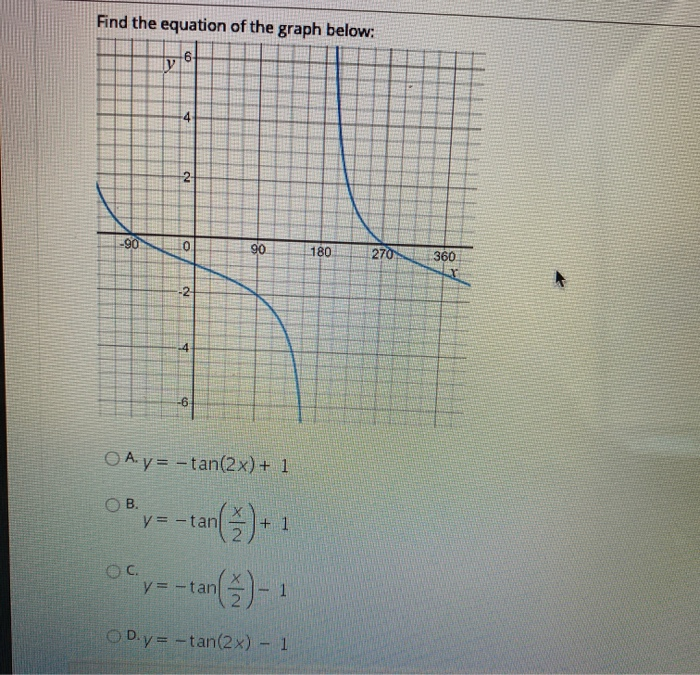


Solved Find The Equation Of The Graph Below 6 Ly 4 2 90 Chegg Com


6 2 Graphs Of Sine Cosine And Tangent Spm Mathematics



Tan Graphs Circular Functions
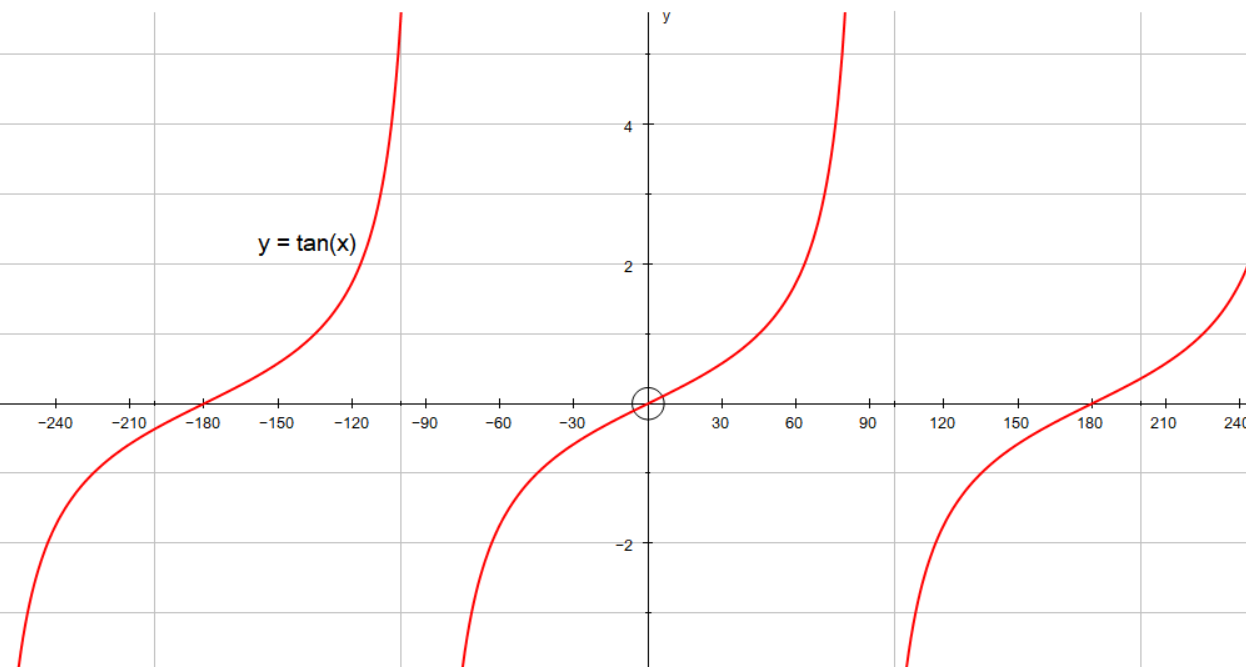


How Do You Graph And List The Amplitude Period Phase Shift For Y Tan X 60 Socratic
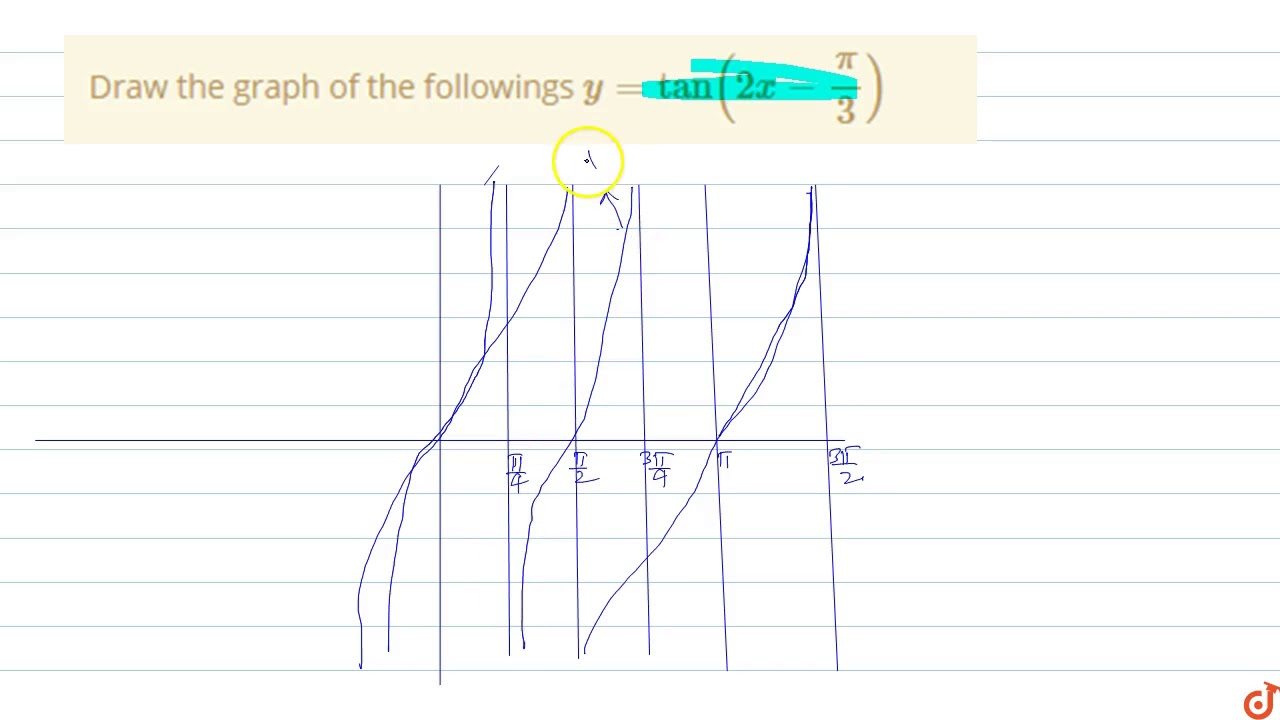


Draw The Graph Of The Followings Y Tan 2x Pi 3 Youtube


Tangent Graphs Worked Solutions Examples Videos


Howto How To Find Vertical Asymptotes Of Tan2x



Tan Graphs Circular Functions



Sketch The Graph 1 Y Cos 2 X 2 Y Tan2x 3 Y Sin2x Maths Trigonometric Functions Meritnation Com


Graphing Y Tan X X 0 Tan 0 X P 4 Tan P 4 X P 2 Tan P 2 X P 4 Tan P 4 X P 2 Ppt Download


Bestmaths
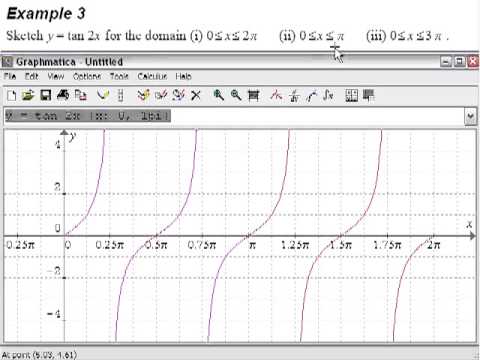


6 Trigonometry Graph Example 3 Sketch Y Tan 2x Youtube



Solved Test 2 Review L A Sketch The Graph Of Y Tan Chegg Com



Draw The Graph Of Y Tan 3x



No comments:
Post a Comment